
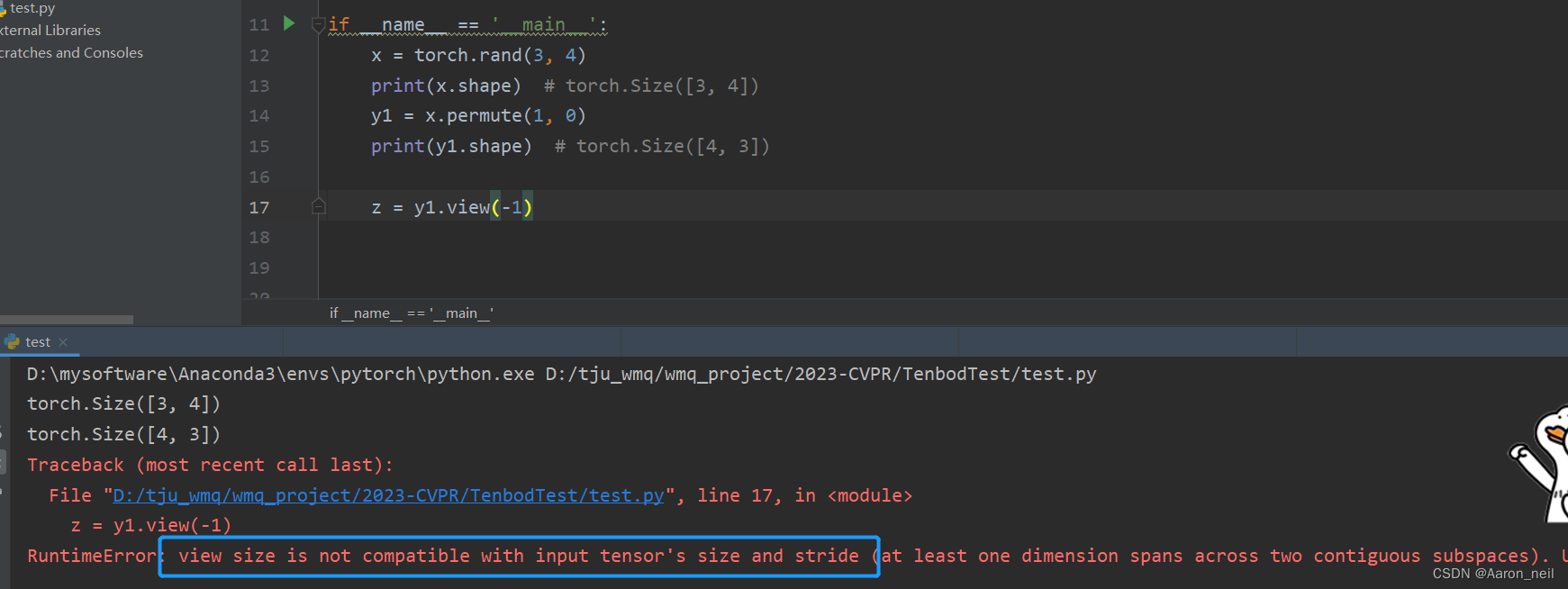
To solve this, simply add contiguous() to a discontiguous tensor, to create contiguous copy and then apply view() bbb.contiguous().view(-1,3) at /pytorch/aten/src/TH/generic/THTensor.cpp:203 RuntimeError: invalid argument 2: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). RuntimeError Traceback (most recent call last) This is probably because view() requires that the tensor to be contiguously stored so that it can do fast reshape in memory. The answer is it the view() function cannot be applied to a discontiguous tensor. So now the question is: what happens if I use a discontiguous tensor? Interestingly, repeat() and view() does not make it discontiguous.
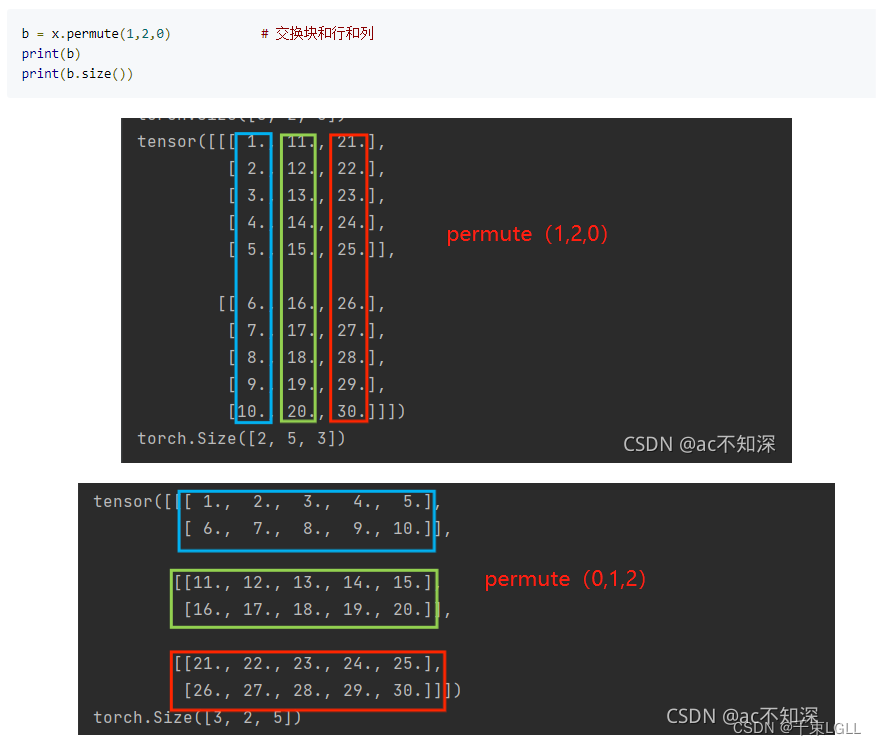
Ok, we can find that transpose(), narrow() and tensor slicing, and expand() will make the generated tensor not contiguous. # means the singleton dimension is repeated d3 timesįff = aaa.unsqueeze(2).repeat(1,1,8).view(2,-1,2) # if a tensor has a shape, it can only be expanded using "expand(d1,d2,d3)", which Now we try apply come functions to the tensor: bbb = aaa.transpose(0,1)Ĭcc = aaa.narrow(1,1,2) # equivalent to matrix slicing aaaĭdd = aaa.repeat(2,1) # The first dimension repeat once, the second dimension repeat twice This indicates that the elements in the tensor are stored contiguously. When moving along the second dimension (column by column), we need to move 1 step in the memory. The stride() return (3,1) means that: when moving along the first dimension by each step (row by row), we need to move 3 steps in the memory. First, let's create a contiguous tensor: aaa = torch.Tensor( ,] ) The contiguous() function is usually required when we first transpose() a tensor and then reshape (view) it. ntiguous() will create a copy of the tensor, and the element in the copy will be stored in the memory in a contiguous way. Some operations, such as reshape() and view(), will have a different impact on the contiguity of the underlying data. The tensor is not C contiguous anymore (it is in fact Fortran contiguous: each column is stored next to each other) > t.T.is_contiguous()Ĭontiguous() will rearrange the memory allocation so that the tensor is C contiguous: We need to skip 1 byte to go to the next line and 4 bytes to go to the next element in the same line. We need to skip 4 bytes to go to the next line, but only one byte to go to the next element in the same line.Īs said in other answers, some Pytorch operations do not change the memory allocation, only metadata. PyTorch's Tensor class method stride() gives the number of bytes to skip to get the next element in each dimension > t.stride() This is what PyTorch considers contiguous. The memory allocation is C contiguous if the rows are stored next to each other like this: Let's consider the 2D-array below: > t = torch.tensor(,, ]) It is not contiguous if the region of memory where it is stored looks like this:įor 2-dimensional arrays or more, items must also be next to each other, but the order follow different conventions. You're generally safe to assume everything will work, and wait until you get a RuntimeError: input is not contiguous where PyTorch expects a contiguous tensor to add a call to contiguous().Ī one-dimensional array is contiguous if its items are laid out in memory next to each other just like below: Normally you don't need to worry about this. When you call contiguous(), it actually makes a copy of the tensor such that the order of its elements in memory is the same as if it had been created from scratch with the same data. Here bytes are still allocated in one block of memory but the order of the elements is different! Note that the word "contiguous" is a bit misleading because it's not that the content of the tensor is spread out around disconnected blocks of memory. In the example above, x is contiguous but y is not because its memory layout is different to that of a tensor of same shape made from scratch. This is where the concept of contiguous comes in. In this example, the transposed tensor and original tensor share the same memory: x = torch.randn(3,2) Narrow(), view(), expand() and transpose()įor example: when you call transpose(), PyTorch doesn't generate a new tensor with a new layout, it just modifies meta information in the Tensor object so that the offset and stride describe the desired new shape.
There are a few operations on Tensors in PyTorch that do not change the contents of a tensor, but change the way the data is organized.


 0 kommentar(er)
0 kommentar(er)
